Abstract

Some fourty-five years ago Shannon proposed a machine that was meant to be able to play an iterated "penny matching" game (a sort of «Odd / Even») and read into its human adversary so as to win : a mind-reading machine. This article sheds some new light on this early machine by comparing various approach to model and anticipate human adversary.  In theory in such complete but imperfect information games (like "heads or tails" or "rock/paper/scissors") the optimal strategy is a mixed one (Nash's theorem). The computation of these mixed strategies presupposes that both opponent are perfectly rational one and may play randomly. This paper analyzes different approach to anticipating human in such games and shows that successful mind-reading machines do take advantage of human difficulty to both play (truly) randomly and his/her limited rationality (problem of memory size, recensy, content, etc). The SAGACE approach we have developed and already presented appears to be the most efficient.

Keywords

Imperfect Information Games, Mind-Reading algorithms, Anticipation, Learning,  Genetic Algorithms.

1. Introduction

In the early 50's, at Bell Laboratories, David Hagelbarger designed a simple ``mind-reading machine”. He was followed by Shannon which improved this first approach (Shannon, 1953). His machine was meant to play an iterated penny matching game against human adversary. In order to win, his machine was supposed to "read" into its human adversary. The game played by the machine is a zero-sum game with two players. Let A be the first player and B the second one. For each move, the players decide in secret and announce simultaneously “heads” or “tails” (or "Odd" and "Even"). If they both announce the same then A wins the move, B otherwise. The game is iterated a pre-fixed number N of times and the winner is the one that has won the greatest number of move.

The rules of the iterated penny matching are very simple and can immediately be understood by a human. There are some obvious similarities (iterated, complete, imperfect) with the well known iterated prisoner dilemma game (Rapoport, 1965). It is a complete and imperfect information game. As such, it is known that an obvious optimal mixed strategy exists (Nash's theorem) : a uniform random choice made each move. Shannon's "mind-reading machine" did outperform significantly humans on average. Even against humans that know the optimal mixed strategy ! We consider that an explanation for such result is that, intuitively,  it is very hard for a human to deal correctly with random. It seems impossible for humans to “generate” series of independent random values. When human players are involved in such a game, they try to anticipate their opponent next move. Even if you tell them that the optimal strategy consist in totally random moves they exhibit patterns that may be detected and used by machines.

This article compares four types of "Mind-reading" programs both theoretically and experimentally against human and against one-another. The results give a possible explanation for Mind-Reading machine success.

The SAGACE approach we have developed and already presented (Meyer and Ganascia, 1996 ; meyer et al., 1997) appears to be the most efficient. It relies on an explicit modeling of the adversary strategy that dynamically evolves.  When it cannot find a winning solution, the system is able to play through a process of anticipation. This is done by building and refining a model of the adversary's behavior in real time during the game. The architecture proposed here relies on two genetic classifiers, one of which models the adversaries' behaviors while the other uses the models thus built in order to play. The results show the advantages of our approach over human and traditional artificial adversaries and illustrate how the system learns the strategies used by its adversaries.

The Shannon Machine consists in an eight state automata that takes into account the previous behaviors of its opponent. In particular, its considers how his opponent adapts his strategy regarding to his victories or defeats after certain moves. It takes also into account changes in strategy and persistence. Without entering into details, what did Shannon is build a program for modeling the human strategy and using this information to win. Adversary modeling is a problem that has received a growing interest (Carmel and Markovitch, 1996; Meyer et al., 1997; Stone and Veloso, 1996).  

Analyzing adversary modeling in the context of  iterated penny matching game raises many questions that are critical on the nature of modeling and anticipation in games. To build "mind-reading machines" it is indeed important to take into account the nature of human memory (structure, size, perenniality, etc.), the use of random (and the problem human random is never uniformly distributed), the representation language for the strategies (finite state automata, grammars, etc.) A key question is also related to the choice of a given modeling language. In certain context, if acquiring the model requires more time than the length of the game, it will be useless.  

The sequel of the paper is divided as follows. Section 2 presents the problem of anticipation met in "mind-reading machines". Section 3 compares different strategies for reading into human adversaries. Section 4 presents some experimental results and a discussion.

2. Mind-Reading Machines (MRM)

2.1. Problem of anticipation in « mind-reading machines »

To compare different strategies used in building MRM, we propose to use several criteria. One first criterion is whether or not the MRM does model the opponent's strategy. We shall call true mind-reading machines the ones that build or have a model of the opponent and false mind-reading machines the ones that do not represent their opponent. The MRM will be the player A and the opponent the player B. One important notion in the iterated penny matching game is a pattern. A pattern of move corresponds to a sequence of couples of the form (ai,bi) where ai is what A has played at the ith move, bi is what B has played. Recall that by definition of the game A wins the  ith move if it plays the same as B, i.e. when (ai=bi). This notion of patterns, allows to express simple strategies such as if ((ai,bi) and ai¹bi ) then ai+1¹ai. This strategy means that after a loss (ai¹bi ), A switch its choice to play a move different from ai  (e.g. you choose odd  if you had chosen even). This strategy does not model explicitly the opponent's strategy but base only its choice on previous results.

 Table 1 presents the other criteria that we are using to characterize the different adversary modeling approaches to the iterated penny matching. 

Table 1: Several criteria for comparing adversary-modeling approaches.

2.2 Examples of existing true « mind-reading machines »

This section presents a set of true mind-reading machines along the criteria presented above. As true MRM, all of them do take into account explicitly or not the opponent’s behavior. A will refer to the MRM and B to the human opponent. NextMove is a predicate such that NextMove(B,M) means that B' NextMove is M (either Odd or Even).

 2.2.1. TitAfterTit MRM:

This is a humorous reference to the famous TitForTat strategy used in the iterative prisoner dilemma (Axelrod, 1984). In this strategy the prediction of the opponent is to consider that the next opponent’s move will be the same as the last one whatever what the result of the previous move. There are only two patterns: opponent just played Even and opponent just played Odd. The TitAfterTit strategy may be expressed as: IF (*,M) Then NextMove(B,M).

 The properties of this strategy along our criteria are summarized in the next table. 

Table 2. TitAfterTit strategy properties

2.2.2. Shannon MRM (Shannon, 1953).

The strategy proposed by Shannon consists in analyzing patterns of length two related to what the opponent played and the success of the moves. A prediction is associated with such patterns. It also takes into account whether or not the patterns have been reproduced at least twice. When there are not enough evidence then it plays uniformly random. Regarding its memory, it may represent the detection of patterns that occurred a long time before. If the prediction associated to a pattern happens to be wrong, the corresponding memories are purely erased. Even if the prediction was correct for many times. Example of pattern: P1 = "Opponent won twice by playing the same move m". Memories associated to pattern P1 are: M1 and M2. M1 stores the prediction that the opponent in a pattern P1 will then play m or . M2 stores a Boolean describing whether or not the pattern P1 and M1 were repeated at least once. The properties of this strategy along our criteria are summarized in the next table. 

Table 3. Shannon strategy properties

2.2.3. Minasi (Minasi, 1991)   

Minasi is a MRM that the authors [2] have illustrated on the famous game of “Paper, Scissors, Rock” which is also a complete and imperfect information game. We adapted it for the ”penny matching'' game. The principle is very simple, the machine records all previous moves and search patterns in its memory that match with the current state of the game. More precisely, this strategy consists in analyzing at each move (number n) the patterns of length at most n during the past (n-1)/2 moves. It then considers the largest repeated pattern and then  plays accordingly (i.e. it considers that the move right after this pattern is a good predictor of the opponent). Examples of patterns (only the largest will be considered for prediction): P1 = O; P2 = E; P3 = OE, P4 = EO, P5 = OEO, P6 = EOOE.

There are no memories associated to patterns, the entire history of move is recorded. The properties of this strategy along our criteria are summarized in the next table.

Table 4. Minasi strategy properties

2.2.4. Sagace (simplified) (Meyer et al., 1997)

The principle of the simplified Sagace method used in this context is similar to Minasi but Sagace takes explicitly into account the consequences of each move. In other words, Sagace does not only detect patterns but is also interested in whether or not these patterns lead to a success for the opponent. The idea is that Sagace will not remember patterns that were unsuccessful for the opponent and therefor may adapt to evolving strategies. Examples of patterns (only the largest will be considered for prediction) are similar to Minasi. 

The memory associated to each pattern takes into account how recent the pattern has been detected during the game. This is an important difference with Minasi. Indeed, while modelling humans the fact that they forget is a key aspect of their memory (Stern, 1985).  The properties of this Sagace along our criteria are summarized in the next table. 

Table 5. Sagace strategy properties

2.2.5. Human

If machines may attempt to read into human's mind, the opposite is also true. Humans may attempt to model the machine. Human strategies for modeling are yet unknown but according to experiments we have been carried out, several features have emerged. There is a kind of modeling that seems to take into account the fact that the human itself is modeled (when we tell him that the machine attempts to identify his strategy). This is also an attempt from the human to adapt his behavior so as to mislead the machine. Moreover, when attempting to play randomly, the human often exhibits a behavior that may be slightly predictable (for example he will do a sequence of EOEOEO thinking that this is perfectly random). The confusion between regular and random is indeed not new. Several properties of human strategies for reading in the machine along our criteria are summarized in the next table. 

Table 6. Human strategy properties

2.3. Examples of false « mind-reading machines » 

Not all machines are considered as true Mind-Reading Machines. A machine using the uniform random strategy is an example of a false Mind-Reading Machine. Its strategy simply consists in playing either even or odd randomly. This strategy does clearly ignore the opponent’s strategy and the issue of the preceding moves. The mixed strategy does also belong to this class of strategies. This strategy is a variant of the previous one. It consists in playing even with a given probability p and odd with the probability (1-p). This strategy does also ignore the opponent’s strategy and the issue of the preceding moves. Other strategies of this kind include the entire one that may be represented using a DFA that takes into account only the previous move played by the machine itself. For example EEàO, OOàE, EOàO, OE->E. (gives the cycle EEOO if initialized with EE). This strategy does also ignore the opponent’s strategy and the issue of the preceding moves.

3. Experimentation

All the true « mind reading machines » we have presented were historically conceived to play against humans. They were human mind reading machines. A natural way to compare these machines could  well be do perform a large series of experimentation’s against selected human opponents and rank the machines according to the results of these experimentation. Nevertheless, nowadays the question may not to read only human minds but also artificial ones programmed by humans. This remark sheds a new light on the possible ways of comparing strategies. Indeed, our goal is to compare the strategies by evaluating them against one another in a similar manner than one that is used for the classical iterative game of the prisoner dilemma (Axelrod, 1984 ; Rapoport, 1965).

For the experimentation, we have implemented Minasi, Shannon and Sagace and did a tournament and average on 10 games of 500 moves for each of the six pairs made of one or two MRM or one MRM and a human. The three MRM played against different human players and the most representative curves corresponding to the results of tests was kept. For each match and for each MRM we have recorded the percentage of true correct prediction of the opponent (true means: when the opponent didn't play randomly). This gives an idea of the modeling ability of the MRM. We also recorded the percent of moves that were done randomly so as to  measure how much correct prediction were made by chance. The Table below presents the results we obtain.

Table 7. Results of the tournaments between MRM

This first table is very instructive. It first shows that the Human is always beaten by MRM. The figures hereafter give a better understanding of the dynamic of this loss. It also shows that the best strategy is SAGACE because it never looses. It is interesting to note that its prediction accuracy is the highest. Shannon relies the most on random whereas Minasi relies the least. Intuitively, we could conclude that Shannon is heavily relying on random to play. Minasi on the contrary is the strategy that relies the most on the modeling and use very little random. SAGACE appears to be the best at modeling opponent but for a certain number of cases it relies on random. It seems that the different strategies differ in both their ability to predict and their use of random.

To measure the overall performance of the different strategies, we have also recorded tables that represent the evolution of the percentage of games won since the beginning of a match.

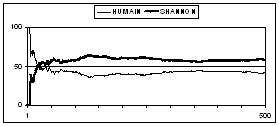
Shannon's strategy needs at least 40 games in order to produce a reliable model of the human player. If play continues, the percentage of games won by Shannon's strategy stabilizes and reaches its extreme limit of 58%. Note that Shannon's machine makes 65% of random moves (see Table 7.).

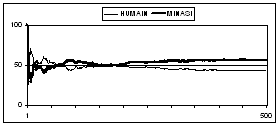
It takes longer for Minasi's strategy to model the human player. The model becomes reliable after 200 games! Minasi's strategy adapts efficiently but very slowly (56% of games won).

 
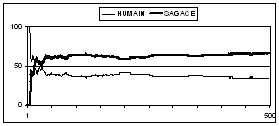
Against the human player, SAGACE adapts very quickly and its final percentage of games won is around 66%. SAGACE appears to be the most efficient. SAGACE is similar to Minasi's strategy but takes explicitly into account the consequences (win or loss) of each move for his opponent. Minasi on the other and is mainly concerned by the analysis of the longest patterns played by the opponent. Whatever was the outcome of each move. Its results prove the importance of such considerations for Humans.

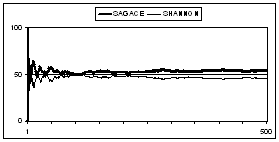
As can be seen in the previous figure, when SAGACE and Shannon's strategy play against each other, the progression in the rate of games won is not monotonic. The two machines seem to adapt continuously to each other. After 100 games, Shannon's machine makes a lot of random moves (see Table 7.). It isn't able to model SAGACE anymore (40% of correct prediction).

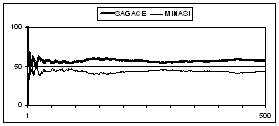
This figure shows how much SAGACE is hard to model. Minasi's strategy uses random for only 6% of its moves and makes only 42% of correct prediction (see Table 7.). SAGACE is still efficient (57% of correct prediction) but we don't have any satisfying explanation for this good result. 

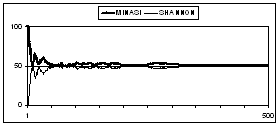
This figure illustrates the problem of misunderstanding! Minasi's strategy and Shannon's one are so different that they do not achieve to adapt against each other. After 200 games, Shannon's strategy "throws in the sponge" and becomes totally random. The percentage of games won by the two players reaches then its theoretical value of 50% (optimal strategy for zero-sum games).

4. Conclusion

This paper has analyzed different approach to anticipating human in complete but imperfect information games and showed that successful mind-reading machines do take advantage of human difficulty to both play (truly) randomly and his limited rationality (problem of memory size, recensy, content, etc.). Four types of "Mind-reading" programs were compared both theoretically and experimentally against human and against one-another.

The results give a possible explanation for Mind-Reading machine success. The results show the advantages of our approach over human and traditional artificial adversaries and illustrate how the system learns the strategies used by its adversaries.

Now, work will be done to find satisfying (if not mathematical) explanations of  SAGACE's success against other MRM and especially against the Minasi's one.

References

[Axelrod, 1984] Robert Axelrod The evolution of cooperation. Basic Books, NY, 1984.

[Carmel and Markovitch, 1996] David Carmel and Shaul Markovitch. Incorporating opponent models into adversary search. Proceedings of the Thirteenth National Conference on Artificial Intelligence, Portland, Oregon, 1996.

[Goldberg, 1989] David E. Goldberg. Genetic Algorithms in Search, Optimization, and Machine learning.  Addison-Wesley, 1989.

[Holland, 1975] John H. Holland. Adaptation in Natural and Artificial Systems.  University of Michigan Press, 1975.

[Holland et al.,  1986] John H. Holland, K.J. Holyoak, P.R. Thagard, and R.E. Nisbet. Induction : Processes of  Inference, Learning, and Discovery. MIT Press, Cambridge, 1986.

[Lorenz and Markovitch,1993] David H. Lorenz and Shaul Markovitch. Derivative evaluation function learning using genetic operators. In Epstein and Levinson, editors. Proceedings of the AAAI Fall Symposium on Intelligent Games: Planning and Learning, Menlo Park, CA. The AAAI Press, 1993.

[Meyer and Ganascia, 1996] Christophe Meyer and Jean-Gabriel Ganascia. S.A.G.A.C.E. Genetic Algorithmic Solution for the Anticipation of Evolving Behaviors. Paris VI,  LAFORIA  N°96/32, 1996

[Meyer et al., 1997] C. Meyer, J-G Ganascia, J-D Zucker. Learning Strategies in Games by Anticipation. Proc of the fifteenth International Joint Conference on Artificial Intelligence, IJCAI’97. Morgan Kaufman editor 1997.

[Minasi, 1991] M. Minasi “Recognizing Patterns”, AI Expert, February 1991.

[Neumann, 1944] John von Neumann and O. Morgenstern. Theory of Games  and Economic Behavior, Princeton University Press, 1944.

[Rapoport, 1965] Anatol Rapoport and A. Chammah. Prisoner's Dilemma. Ann Arbor, University of Michigan Press, 1965.

[Shannon ,1953] C.E. Shannon ; “A Mind-Reading (?) Machine”, Bell Laboratories Memorandum, March, 1953.

[Stone and veloso, 1996] Peter Stone and Manuela Veloso. Towards Collaborative and Adversarial Learning: A Case Study in Robotic Soccer. IJHCS. 1996

[Stern, 1985] Leonard Stern. Structures and strategies of human memory. Dorsey Press. 1985.

[Waterman and Hayes-Roth, 1978] D. Waterman and F. Hayes-Roth. Pattern-Directed Inference Systems. Academic Press, 1978.