Abstract
Game Theory is mainly seen as a mathematical theory which tries to replace pure chance and intuitive behavior in a competitive situation by calculations. This theory has been widely used to define computer programs. The aim of the research described here is to design an artificial system which is able to play efficiently certain games to which Game Theory cannot be applied satisfactorily (such as games with incomplete or imperfect information). When it cannot find a winning solution, the system is able to play through a process of anticipation. This is done by building and refining a model of the adversary's behavior in real time during the game. The architecture proposed here relies on two genetic classifiers, one of which models the adversaries' behaviors while the other uses the models thus built in order to play. The system's strategy learning ability has been tested on a simple strategic game. The results show the advantages of this approach over human and traditional artificial adversaries (simple probabilistic and adaptive probabilistic) and illustrate how the system learns the strategies used by its adversaries.
1. Introduction
Despite its name, Game Theory, which is the branch of operational research dealing with decision taking in a competitive situation, is not only about play activities such as chess or bridge. All strategic activities, so-called because they require the coordination and organization of forces against adversity, are involved, be they questions of diplomacy, politics, industrial choices, economic or military policy. Like all branches of operational research, Game Theory is mainly seen as a mathematical theory which tries to replace pure chance and intuitive behavior in a competitive situation by calculations. If we suppose that those in competition with each other are all trying to optimize their respective advantages, how should the most efficient lines of play be determined ? This is the generic question to which Game Theory tries to find an answer.
Having said this, Game Theory addresses different points of view depending on the type of game and the optimization criteria taken into account. Traditionally, games fall into two categories, depending on whether the information is complete or incomplete, i.e. whether or not the players have full knowledge about the game. Thus chess is a game with complete information while bridge is one with incomplete information. Another distinction is whether the information is perfect or imperfect. It is perfect if the players control all the parameters of the game, as in chess, and imperfect if, for example, two players have to make a move simultaneously without knowing what move the other is making. The optimization criteria also vary depending on whether the adversaries wish to minimize the risk of losing or maximize the chance of winning while trying to avoid a draw, if possible.
In the past, mathematical theories on games went back to the origin of probability theory for games based on pure chance, i.e. with no competitor other than fate. Mathematical theory on games was developed in the 20th century with the work of Emile Borel, followed by that of Von Neumann and Morgenstein in the forties [Neumann and Morgenstern, 1944], then Nash in the fifties. The last three invented the concepts of mini/max and the search for a point of equilibrium that are the basis of what today is called Theory of Game.
With the appearance of the first computers, Game Theory was seen to be an appropriate formalism for the design of game machines in the case of games with complete and perfect information. In this framework the task of the computer was to simulate the predictable futures, while supposing that the adversaries themselves play in a way that is totally rational and try to optimize their advantages. Such a simulation supposes the exploration of all (or most) possibilities in a search tree. When this simulation becomes impossible because of the size of the tree, heuristics are introduced to get round the combinatorial explosion and the machine must presume that the adversaries adopt similar heuristics. Thus most chess playing machines rely on the mini/max algorithm and a common assessment function which takes into account the state of the chess board as it would be after a near exhaustive exploration of a number of moves [Fürnkranz, 1996].
However, despite the undoubted success of this method, a number of problems exist. The first one is that games with complete and perfect information are not the only competitive situations which might benefit from the contribution of computer simulations. And yet, with the notable exceptions of the poker program designed by Waterman using production rule systems [Waterman and Hayes-Roth, 1978] and the one designed by Findler [Findler, 1977], most computer programs have tackled games with complete and perfect information. Note that existing simulations of games such as Mastermind or Scrabble are not strictly speaking games since there is no strategic dimension involving competition. The second is that nothing proves that when games with complete and perfect information are strongly combinatorial they benefit from Game Theory inspired mini/max processing methods. In this case computer simulation is far from covering all possibilities and therefore the presumed rationality of the adversaries is just an illusion. In a word, it would be a good idea to contemplate other types of games with methods other than those inspired by Game Theory. This would make it possible not only to build more efficient programs where machines currently operate but also to extend the empire of computer programs to competition situations such as the design of interactive interfaces which have not really been simulated before.
It is the above considerations that led to considering a new line of research in which adversarial behaviors are no longer computed from a more or less long list of possible behaviors but are inferred from the adversaries' past behavior. The progress over the last few years in the design of adaptive learning algorithms, with the help of genetic algorithms, has made it possible to make such inferences thanks to which the machines build for themselves an internal representation of their adversaries. We set apart from the mainstream approach in ‘Learning in games’ which consist in learning an evaluation function [Lorenz and Markovitch,1996].
Once this representation has been built it has to be used in order to act and this is done through the anticipation mechanism which is presented in this article. In fact, the article is divided into three sections and a conclusion. The first presents the general concepts of inference and anticipation on which the approach is based. The second describes the SAGACE system (Genetic Algorithmic Solution for the Anticipation of Evolving Behaviors) which implements this model with the help of genetic algorithms and the game ALESIA on which SAGACE will be assessed. The third reports on tests which show that when humans play against such a machine they are rapidly beaten by the ability of the machine to predict their reactions. Other tests assess different specially implemented strategies. In particular, it is shown that the behaviors predicted by Game Theory appear as the fixed point extremes of the behavior of SAGACE which, in this sense, has implemented a generalization of Game Theory to non rational adversaries.
2. The new approach
2.1 General overview
The aim of the research described here is to design an artificial system which is able to play efficiently certain games to which Game Theory cannot be applied satisfactorily. The system has been provided with two essential features. The first is that it does a comprehensive scan, to a certain depth, of all possible future states of play according to its actions and regardless of those of the adversary (thus making it possible to identify a possible short term winning strategy). The second is that when it cannot find a winning solution it plays according to a model of the adversary's behavior which it builds and refines in real time during the game. This modeling allows it to anticipate the adversary's actions. As opposed to the work of Carmel and Markovitch [Carmel and Markovitch, 1993], our approach doesn’t consist in learning the evaluation function of an adversary (to be used in a mini/max algorithm) but to construct an real-time behavioral model of this adversary.
The system is built around SAGACE, an original learning method based on inference, modeling and anticipation which enables it to learn both an adversary's strategy and the way this strategy evolves.
2.2 SAGACE
This algorithmic method is implemented in the form of a classifier system [Holland et al., 1986], the rules of which evolve thanks to a genetic algorithm [Holland, 1975], [Goldberg, 1989], and is based on a purely behavioral approach. It predicts and anticipates the behavior of an individual (human or artificial) but does not claim to be able to discover the underlying cognitive or algorithmic mechanisms [Meyer and Ganascia, 1996a]
2.2.1 General architecture
The system is made up of several components which interact in order to determine the most judicious action for each move.
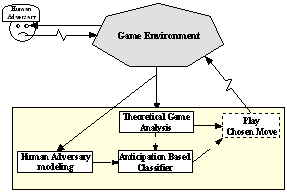
Figure 1. General Architecture
2.2.2 The theoretical analysis component
The role of this component is to manage the theoretical knowledge obtained mathematically using Game Theory. It is used to analyze a given game situation and to determine whether or not it corresponds to a winning position, i.e. whether a pure winning strategy exists. In this way, whenever a winning strategy is identified it is adopted by the system.
If no winning solution is identified, the system tries to use its model of the adversary.
2.2.3 The anticipation component
Each time the system takes a decision the anticipation component determines whether or not the model it has of its adversary is satisfactory, based on certain criteria concerning the accuracy and error rate of past predictions. If the degree of prediction is considered to be satisfactory (above a predefined anticipation confidence rate), the component provides a list of the adversary's most probable actions. Using the list, the component goes on to determine the most suitable move, with the help of a classifier system. Each classifier of the anticipation component is of the form:
'Game_situation & prediction_action_adversary à action_to_be_performed'.
Note that as classifiers these rules are genetically evolutive and therefore adaptive.
If the degree of prediction is considered to be unsatisfactory (below the confidence rate) the system determines its actions by considering that the adversary is likely to make any valid move. In this case the 'prediction_adversary_action' part of the classifiers is undetermined.
2.2.4 The modeling component
The modeling component records in real time all the decisions taken by the adversary according to the configuration of the game. Modeling is performed by creating the adversary's behavior rules and then adjusting them regularly so as to reflect the real attitude of the adversary as faithfully as possible. These rules are also managed like classifiers and have the following form:
'Game_situation à action_performed'.
When, in similar circumstances, the adversary repeats an action he has already performed, the modeling component increases a confidence coefficient linked to this action in this configuration. If the action is different, a new behavior rule is created.
Two coefficients are added to the behavior rules, their role being to give information about the frequency of use and success rates of the rules w.r.t to the modeled player. If, for example, a modeled player often performs a certain action in a given context but with a negative effect, then the coefficient of the frequency of use of the corresponding behavior rule will be high whereas that of the success rate will be low. In addition, the coefficients are given a time weighting. The fact that an action has been chosen recently is more important than if it had been chosen much earlier. Similarly, if the behavior of a modeled player was successful in the past but has recently turned out to be inappropriate, the success rate coefficient will depend more on recent results than on past ones and will certainly be low. Management of this time weighting can be parametrized according to the degree to which the built model of the adversary corresponds to his real observed behavior.
In any situation the system can thus send a request to this component in order to get some idea of how the adversary will play.
3. Tests
In order to assess this new approach, an artificial player called Sagace was designed to play against different types of adversary at a repeated game with complete and imperfect information. This game is called ALESIA and is described below.
3.1 Alesia
Alesia is a game between two players who have to try and push the marker across the board to the other one's citadel. At best this can be done in three consecutive winning moves. At the beginning of the game each player receives a capital of 50 points. The players decide in secret and announce simultaneously how many points (at least one and at most their capital) they have decided to play during a given move. The player who announces the highest number pushes the marker (initially at the center) one slot towards the adversary's citadel. If they both announce the same number, the marker remains where it is. In both cases the number of played points is deducted from the players' capital. A player wins if he manages to move the marker to the adversary's citadel. Otherwise it is a draw.
This game contains a number of interesting features. The rules are very easy and can very quickly be understood by a human, the information is complete and imperfect and there is no general non-mixed winning strategy (this has been proved mathematically).
3.2 Implementation
The system has been implemented in Delphi 2.0 for Windows 95 and it is possible for two computer players to play 1000 games in about 30 seconds on a Pentium Pro PC. Thus a large number of series of tests have been run to assess system performance. For each adversary (human or simulated) of the system there is a modeling base and an anticipation base (to begin with it is the same for all adversaries but is likely to evolve differently for each).
The classifiers contained in the modeling bases are encoded in the form 'Condition -> action'. The 'condition' part is made up of intervals of possible values for the number of points of the two opponents and the position of the marker. The 'action' part indicates the number of points to be played.
The anticipation base classifiers are encoded in the same formalism with just an additional indication in the 'condition' which encodes the prediction of the adversary's action. These classifiers have, for the most part, been elaborated by a human player using introspection and then encoded in the formalism imposed by the form of the classifiers. Others have been built after looking at the behavior of good players and have in fact been taken from the modeling bases of certain particularly successful players. This idea has already been studied concerning the bootstrapping of a classifier system [Meyer, Ganascia 1996b].
4. Results
A test protocol has been defined involving three specific groups of adversaries for Sagace. This set of players seems to be sufficiently varied so as to represent the different strategies that a human player could try and adopt when playing Alesia. Sagace has therefore been set against real humans, simulated non- adaptive probabilistic players and simulated adaptive probabilistic players (the exact nature of which will be described below). Each of the tests measures the evolution in the percentage of games won since the beginning of the session.
4.1. Human adversaries
The system played against different human players and the most representative curve corresponding to the results of this series of tests was derived. Each human played a hundred games (Figure 2).
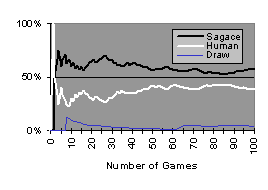
Figure 2. Human adversaries
As can be seen in figure 2, the progression in the rate of games won by the players is not monotonic. The two players seem to have continually adapted their way of playing to the other. After 85 games the human player no longer seems capable of imagining new strategies adapted to Sagace and the rate of games won by the latter rises slightly. Longer series of games against different players show that the curves end up stabilizing, in general around the same values as those shown in figure 2 (55% for Sagace and 45% for the human player). It is difficult to interpret this type of curve but what is clear is that both human and machine adapt very quickly to each other. It is also clear that the intensity of the variations decreases with the number of games.
If the system uses exactly the same components with the same classifiers when the adversary modeling component is disabled, the human wins more than 80% of the games. This result proves the importance of modeling and anticipating.
4.2 Probabilistic adversaries
In the second type of test the system played against simulated players with probabilistic strategies. Since these strategies rely on chance, they naturally come to mind when a human is trying to thwart the modeling he knows he may be the subject of. The first of these adversaries is a probabilistic player who plays at random a number between one and the number of points he has left.
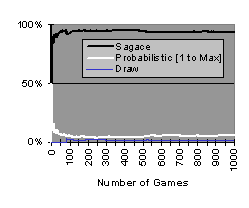
Figure 3. First probabilistic adversary
Very quickly Sagace analyzes the situation, generates a very reliable model of this adversary and adapts perfectly (Figure 3).
The second adversary is also probabilistic but always chooses a number between 1 and 50. If the number that is computed is greater than the number of points he has left, he plays all his remaining points.
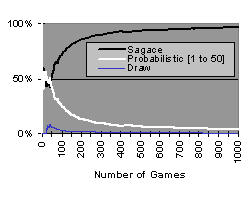
Figure 4. Second probabilistic adversary
It takes longer to model this player than the previous one and the results are not as good at the beginning but better at the end (Figure 4). Modeling is more tricky (convergence is slower) because there is no equiprobability in the choices of action as the higher moves are naturally favored. After fifty games, however, the model elaborated by Sagace is very reliable.
The third adversary simulates an expert theoretician and is able to recognize mathematically when a situation allows a winning strategy, which will always be played. Otherwise his behavior is determined by a set of probabilistic rules that have been introduced according to a games expert (e.g. 'never play more than one point above your adversary's remaining points').
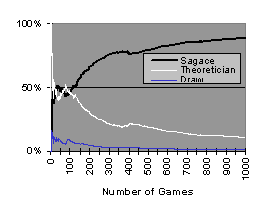
Figure 5. Theoretician adversary
Sagace needs at least 150 games in order to produce a reliable model of this player (Figure 5). Before that there is a period during which the players are equal, during the following 150 games Sagace plays very well, and then the percentage of games won stabilizes. If play continues, the percentage reaches its extreme limit of 85%.
4.3 adaptive adversaries
In the third type of test the system played against simulated players with adaptive strategies. These strategies naturally come to mind when a human is trying to thwart the modeling he knows he may be the subject of by dynamically modifying his strategies. The simulated adversary is a player who will adapt his strategies according to results. This player has been implemented in the form of a classifier system; it learns through the traditional method of positive and negative retribution of the rules governing choice of action ac cording to results [Holland et al., 1986].
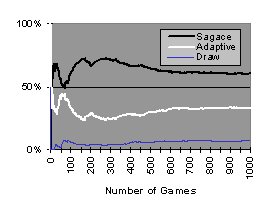
Figure 6. Adaptive adversary
During the first fifty games, Sagace manages to model the adaptive player relatively well and the percentage of games won increases (Figure 6). During the following fifty games the adaptive player adapts, then Sagace manages to determine a new consistent model and the percentage of games won increases again. After a certain number of these 'adaptation' swings the percentage of games won stabilizes (60% for Sagace, 40% for the adaptive player). Note that this type of player is less efficient than a good human player.
4. Discussion
Thanks to the architecture of this system it is possible to be free of the limitations of caution imposed by Game Theory while at the same time taking advantage of its mathematic results when they are optimal. Yet this method offers no theoretical guarantee of results, unlike Game Theory. In fact, it is a different way of apprehending the inequation between security, risk and results. Against any adversary with a fixed strategy this approach is formidable since it can determine the adversary's behavior rules and choose the appropriate strategies. Against an adaptive adversary, the efficiency of the system naturally depends on the degree of adaptability of the adversary. A priori, one would assume that a human is a highly adaptive adversary and yet human players are often beaten by the system. When a human player is informed of the type of learning process used by the system he often tries to adopt a strategy that is very different from his original one. Either he tries to make himself unpredictable by playing more or less at random (but this will often make him make moves that are not optimal and he will lose) or he will try and deceive the system by playing the same move several times over and then changing as soon as he thinks the system is going to play according to this information that he has deliberately given. In fact, these human players model the system that is trying to model them. This human strategy requires great perspicacity and heavy concentration but may be extremely successful.
5. Conclusions and future lines of research
Not only does this approach involving repeated games with complete and imperfect information not challenge mathematically valid results but it also offers a solution to address/apprehend complex situations in which it is important if not essential to have a reliable model of individuals or agents with which one interacts.
The system will be improved by giving it means to model itself so as to be able to tell when it has become predictable and thus change behavior accordingly. This improvement will also make it possible to analyze more rigorously the way the system learns.
In addition, work will be done to see how to adjust the probabilistic coefficients of an optimal mixed strategy that has been determined using Game Theory, according to the way SAGACE models the behavior of its adversaries.
Also, some of the ideas concerning the generalization of genetic rules in classifiers will be implemented so as to extend the predictions of an adversary's actions to situations that have not actually been observed but are similar.
Finally, extension to more complex games (chess, poker) and to cooperative games (iterated prisoner’s dilemma) will be studied.
References
[Carmel and Markovitch, 1996] David Carmel and Shaul Markovitch. Incorporating opponent models into adversary search. In Proceedings of the Thirteenth National Conference on Artificial Intelligence, Portland, Oregon, 1996.
[Findler, 1977] Nicholas V. Findler. Studies in machine cognition using the game of poker. Communications of the ACM, 20(4):230-245, 1977.
[Fürnkranz, 1996] Johannes Fürnkranz. Machine learning in computer chess: The next generation. ICCA Journal, 19(3):147-160, September 1996.
[Goldberg, 1989] David E. Goldberg. Genetic Algorithms in Search, Optimization, and Machine learning. Addison-Wesley, 1989.
[Holland, 1975] John H. Holland. Adaptation in Natural and Artificial Systems. University of Michigan Press, 1975.
[Holland et al., 1986] John H. Holland, K.J. Holyoak, P.R. Thagard, and R.E. Nisbet. Induction : Processes of Inference, Learning, and Discovery. MIT Press, Cambridge, 1986.
[Lorenz and Markovitch,1993] David H. Lorenz and Shaul Markovitch. Derivative evaluation function learning using genetic operators. In Epstein and Levinson, editors. Proceedings of the AAAI Fall Symposium on Intelligent Games: Planning and Learning, Menlo Park, CA. The AAAI Press, 1993.
[Meyer and Ganascia, 1996a] Christophe Meyer and Jean-Gabriel Ganascia. S.A.G.A.C.E. Genetic Algorithmic Solution for the Anticipation of Evolving Behaviors. Paris VI, LAFORIA N°96/32, 1996.
[Meyer and Ganascia, 1996b] Christophe Meyer and Jean-Gabriel Ganascia. Utilization of imitation and anticipation mechanisms to bootstrap an evolutive distributed artificial intelligence system. Animal Societies as an Alternative Metaphorical Basis for DAI - Workshop ICMAS, 1996.
[Neumann and Morgenstern, 1944] John von Neumann and O. Morgenstern. Theory of Games and Economic Behavior, Princeton University Press, 1944.
[Waterman and Hayes-Roth, 1978] D. Waterman and F. Hayes-Roth. Pattern-Directed Inference Systems. Academic Press, 1978.